Использование анализа чувствительности реагирования в процессе оценки риска инвестиционного проекта

Построим задачу, двойственную нашей.

Пусть p1 — двойственная оценка фондов в первый год;

p2 — двойственная оценка фондов во второй год.

В этих обозначениях, необходимо минимизировать общие альтернативные стоимости совокупного объема фондов в целом за период проекта, т. е. минимизировать функцию

Z = (40 000 p1+ 30 000 p2)

при следующих ограничениях:

100p1+ 200 p2 ≥ 400;

300p1+ 100 p2 ≥ 500;

Экономический смысл ограничений состоит в том, что продажа всех ресурсов (фондов), затрачиваемых на единицу каждого вида оборудования (факса или ксерокса) по их альтернативной стоимости в сумме не может быть меньше чистого дисконтированного дохода от одного факса или ксерокса (соответственно). Кроме того, альтернативные стоимости, как реальные экономические величины, не могут иметь отрицательных значений, поэтому: p1 ≥ 0; p2 ≥ 0;

Уже этот простой пример наглядно демонстрирует возможности и преимущества использования методов математического программирования для принятия проектных решений.

Экономико-математическая сущность анализа чувствительности состоит в следующем:

на основе базового варианта проекта определяют ожидаемое среднее отклонение каждой переменной величины (фактора) и результаты проекта в случае отклонения одной из переменных величин от базового сценария. Предполагают, что проект более чувствителен к изменению одного из параметров базового варианта, чем другого, если отклонение первого параметра дает большее отклонение критерия NРV — чистого дисконтированного дохода проекта (или другого критерия, выбранного для оценки) по сравнению с базовым сценарием.

Построим количественный показатель чувствительности проекта sens(у,хi). Пусть у — некоторый критерий эффективности проекта. Он может быть функционально выражен через параметры проекта хi, т.е.

у = у(x1,x2, .,xk-1, xk).

В качестве показателя чувствительности проекта к изменению параметра х, рассчитаем отношение относительного приращения критерия к относительному приращению параметра:

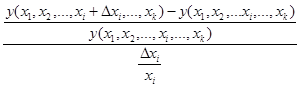
Однако при различных (дискретных) значениях будут получаться различные значения чувствительности. Чтобы этого не происходило, будем уменьшать так, чтобы в интервале функция у (хi) при неизменных прочих х приближалась к касательной в точке хi , тогда

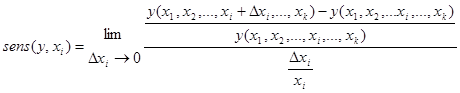
Величина sens (у, хi) показывает, на сколько процентов изменится значение критерия у проекта при изменении параметра хi на один процент.

Пример. Рассмотрим проект строительства нового завода по производству лазерных дисков.

Первоначально требуется вложить денежные средства в строительство завода и покупку технологии. Первоначальные затраты представляют собой фиксированное значение величины С0 , которая инвестируется сразу в момент времени t = 0.

Предположим, что ежемесячный выпуск будет постоянным и равным N лазерных дисков в месяц при постоянной же себестоимости Y, тогда ежемесячные издержки по выпуску равны NY. Пусть ежсмесячные постоянные издержки составят F. Производство лазерных дисков нaчнется через п месяцев после начала проекта.

Денежные поступления (выгоды) от проекта будут идти только в виде выручки от продажи продукции и цена Р одного лазерного диска постоянна во времени. Длительность проекта во времени не ограничена.

Чистый дисконтированный доход (NPV) проекта можно рассчитать на основании следующего уравнения:

, где r – ставка процента

Упростив формулу, получим: